
In our base-10 number system, each digit represents a count of a certain value associated with its place in the number. The long arithmetic algorithms are rooted in the concept of place value. Long arithmetic is used to solve addition, subtraction, multiplication and division problems in writing, often by organizing numbers one on top of the other, with digits aligned in columns. We have also developed detailed step-by-step solutions for long division of whole numbers and negative numbers as well as-for the high-school level-multiplication and division of polynomials.
HTTP WOLFRAMALPHA PRO
Now, Wolfram|Alpha Pro returns step-by-step solutions for long addition, subtraction, multiplication and division problems, including ones involving decimals or negative numbers. A fifth grader will not only be expected to “fluently multiply multi-digit whole numbers using the standard algorithm,” but also “add, subtract, multiply, and divide decimals.”
HTTP WOLFRAMALPHA HOW TO
The Common Core State Standards for mathematics indicate that first-grade students should learn how to add “a two-digit number and a one-digit number.” By second grade, students “add and subtract within 1000” and, in particular, “relate the strategy to a written method.” In third grade, multiplication by powers of 10 is introduced, and by fourth grade students are tasked to “use place value understanding and properties of operations to perform multi-digit arithmetic,” including multiplication and division. In the past several decades in the United States, long arithmetic has traditionally been introduced between first and fifth grade, and remains crucial for students of all ages. But what ultimately made Wolfram|Alpha possible was a singular commitment to the goal of making all the world's systematic knowledge computable.In grade school, long arithmetic is considered a foundational math skill. Wolfram|Alpha's world-class team draws from many fields and disciplines and has unique access to experts across the globe. But to build it required not just unique technology and ideas, but also the experience of 30 years of long-term R&D and ongoing development of robust technology at Wolfram Research. Wolfram|Alpha represents a substantial technical and intellectual achievement. But still more important is that the very paradigm of NKS was crucial in imagining that Wolfram|Alpha might be possible. Many specific ideas from NKS-particularly those related to algorithms discovered by exploring the computational universe-are used in the implementation of Wolfram|Alpha. With a world-class team and participation from top outside experts in countless fields, we are constantly working to create what we hope will stand as a major milestone of twenty-first century intellectual achievement.īeyond Wolfram Language, another key to Wolfram|Alpha is A New Kind of Science (NKS). We work to accept completely free-form input, and to serve as a knowledge engine that generates powerful results and presents them with maximum clarity.Įnergetically developed for more than a decade, Wolfram|Alpha is an ambitious, long-term intellectual endeavor that we intend will deliver ever-increasing capabilities over the years to come.
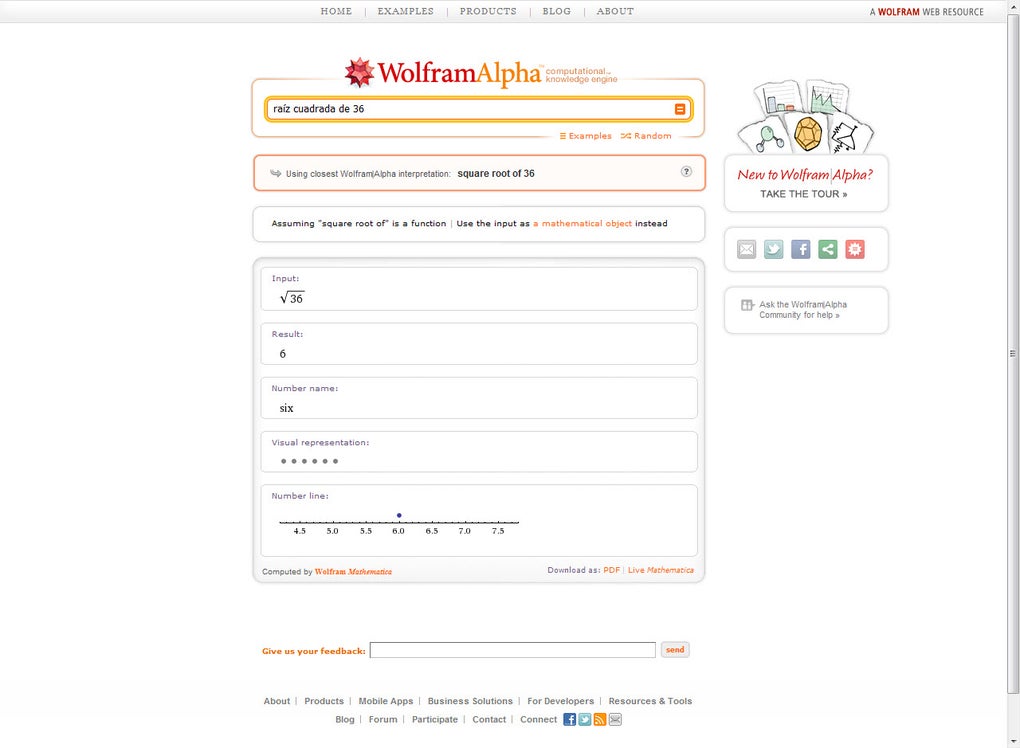
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people-spanning all professions and education levels. Our work builds on the achievements of science and other systematizations of knowledge to provide a single source that can be relied on by everyone for definitive answers to factual queries.


Our mission is to collect and curate all objective data implement every known model, method and algorithm and make it possible to compute whatever can be computed about anything.


 0 kommentar(er)
0 kommentar(er)
